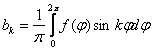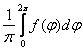Методы получения размеров. Заданные размеры могут быть выдержаны при
наладке технологической системы:
индивидуальной, при которой каждую деталь
обрабатывают после новой наладки (к ней относят наладку путем пробных рабочих
ходов и измерений);
партионной,
называемой также способом автоматического получения размеров, при котором
заданную партию деталей обрабатывают после одной наладки; к ней относят
обработку осевым инструментом (сверлами, зенкерами, развертками, протяжками),
обработку деталей на предварительно налаженных токарных, фрезерных и других
станках. К этому же способу относят обработку на автоматическом оборудовании
(станки с ЧПУ, станочные гибкие производственные
системы и т. п.) с применением систем автоматического управления и контроля. В
этом случае можно уменьшить не только допуск размера (отклонения размера не
превышают 2-40 мкм), но и допуск формы и расположения обрабатываемых
поверхностей (отклонения не превышают 5 — 20 мкм).
Различают два способа получения размеров заготовки:
индивидуальный, когда точность заготовок зависит от произвольного сочетания условий
изготовления каждой отдельной заготовки (например, для отливок - от плотности
и точности форм, для поковок, выполненных ковкой,— от условий ковки, от
профессиональных навыков и качества работы оператора);
автоматический, когда точность заготовок определяется погрешностями регулирования,
наладки соответствующего оборудования, точностью изготовления инструмента,
влиянием нарастающего износа инструмента (литье под давлением, получение
заготовок штамповкой в штампах).
Способы получения размеров заготовок и деталей при механической
обработке тесно связаны между собой. Заготовки, полученные индивидуальным
способом, обычно устанавливают на станках с помощью выверки. Положение
инструмента также обеспечивают индивидуальным способом. Обработка на автоматическом
оборудовании (автоматических линиях, автоматах, станках с ЧПУ, в том числе
встроенных в гибкие производственные модули и системы) проводится способом партионной наладки технологической системы. В этом случае
необходимо иметь более точные заготовки вне зависимости от программы выпуска
изделий.
Эти особенности получения размеров учитывают при определении
элементарных погрешностей установки заготовок для обработки, наладки
технологических систем и т. п., а также при определении суммарной погрешности
обработки.
Модель. Для изучения и выявления закономерностей процессов обработки
деталей часто прибегают к их исследованию с помощью моделей, отражающих
основные свойства объектов моделирования. Изучение свойств объекта
моделирования с помощью анализа аналогичных свойств его модели представляет собой
процесс моделирования. Различают физические и математические методы моделирования
Физическое моделирование предназначено для исследования натурных моделей
подобия, воспроизводящих объект моделирования в меньшем масштабе.
Математическое моделирование основано на том, что реальные процессы в объекте
моделирования описывают определенными математическими соотношениями,
устанавливающими связь между входными и выходными воздействиями. Математическое
моделирование, сохраняя основные черты протекающих явлений, основано на
упрощении и схематизации. Математические модели являются моделями неполной
аналогии.
Для успешного использования модели необходимо, чтобы она количественно
и качественно верно описывала свойства объекта моделирования, т. е. она должна
быть адекватна.
В зависимости от метода получения математических соотношений различают
модели: статистические, основанные на описании физических и химических
явлений, и смешанные.
Модели смешанного типа для решения технологических задач строят на
основании описания физических процессов в объекте моделирования, однако ряд
коэффициентов определяют экспериментально.
Расчет погрешности обработки детали по данному параметру (размеру,
отклонениям формы, расположения и т. п.) состоит из трех этапов. На первом
этапе проводят схематизацию реальной операции. Далее
выполняют теоретический анализ операции, в результате которого устанавливают
зависимости для расчета элементарных и суммарной погрешностей. На
третьем этапе экспериментально проверяют полученные соотношения.
Анализ точности с полным учетом всех факторов невозможен, поэтому при
схематизации операции (выборе расчетной схемы модели) обосновывают
возможность учета факторов, которые наиболее заметно влияют на рассматриваемый
параметр точности обработки.
Так, при расчете погрешности базирования обычно пренебрегают
отклонениями формы поверхности заготовок, служащей базой. Такая схематизация
часто оправдана, но не для всех операций. Например, при обработке валов,
устанавливаемых в люнете, погрешности формы поверхности, используемой в качестве
базы, копируются на обработанном профиле детали, поэтому расчетная схема здесь
должна быть иной.
При оценке отклонений размера цилиндрической поверхности, возникающей
из-за упругих деформаций технологической системы, ограничиваются анализом
влияния постоянной (в пределах одного оборота) составляющей силы резания; для
объяснения механизма возникновения отклонений формы и расположения
обработанного профиля и их оценки необходим анализ системы в динамике. Таким
образом, вид рассматриваемого параметра точности может решительным образом сказаться
на модели процесса.
При анализе точности обработки технологическую систему обычно
рассматривают как линейную динамическую систему. Это позволяет получить явные
решения в замкнутой форме. Термин «динамическая система» указывает на то, что
процессы в этой системе протекают во времени. Динамическая система может быть
нелинейной, но поскольку исследуется точность обработки, при которой смешения
невелики, то систему можно рассматривать как линейную.
Внешние возмущения, действующие на входе в систему или в элементы
системы, называют входными переменными, сигналами или функциями. На выходе
наблюдают выходные переменные, сигналы или функции. При работе системы каждой
комбинации входных функций [вектору x(t)] соответствует
определенная и единственная комбинация выходных функций [вектор у(t)]. Закон, по которому x(t) соответствует
y(t), называют оператором; обозначим его через А:
y(t) = Ax(t).
Система линейна, если линеен ее оператор. Оператор А называют линейным, если при любых
числах n, с1,...,сn, и любых функциях x1(t),..., xn(t) справедливо равенство
 ,
,
которое отражает свойства однородности и независимости
действия факторов (наложимости воздействий,
суперпозиции, аддитивности). Понятие
однородности означает, что реакция системы на любой сигнал, умноженный на
некоторую постоянную, равна этой постоянной, умноженной на реакцию системы на
входной сигнал. В соответствии со свойством суперпозиции реакция системы
(перемещения, напряжения и деформации) на сумму входных сигналов (сил или
тепловых воздействий) не зависит от порядка приложения сил или тепловых полей
и равна сумме реакций на каждый отдельно взятый входной сигнал. При этом
подразумевают, что модуль упругости E и температурный коэффициент линейного расширения α, не зависят от напряжения и температуры.
Упрощение расчетной схемы, рассмотрение ее как линейной с присущим ей
свойством суперпозиции открывают широкие возможности для упрощения расчетов
динамических систем. Возможность рассмотрения технологической системы как линейной
позволяет разработать наглядную и логичную теорию точности, основанную на
дифференцированном анализе простейших элементов технологического процесса или
операции. При этом полностью раскрывается физическая сущность этих элементов.
Обязательным условием является возможность описания этих элементов аналитически.
Действующее на технологическую систему воздействие в большинстве
случаев имеет четко выраженный период колебаний Т. Так, произвольно заданное внешнее силовое воздействие P(t) (или тепловое) представляют совокупностью некоторых
однотипных составляющих; далее определяют эффект действия одной из
составляющих. Общий эффект от действия силы P(t) образуется
как соответствующая сумма частных. Применяют различные варианты разложения
силового воздействия. Чаще всего силу представляют в виде конечной суммы
гармонических составляющих (применяют разложение в ряд Фурье):
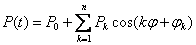 .
.
Теория точности построена на разумном сочетании дифференцированного
подхода к изучению отдельных типовых простейших элементов и обязательного
комплексного охвата всех сторон, всех операций и переходов обработки,
транспортирования заготовок при обработке, контроля заготовок и деталей. Требование
комплексности важно при анализе комплексно автоматизированных производств
(автоматических линий, гибких производственных систем).
Требование комплексности реализуется в нескольких
направлениях: учетом совокупности основных факторов, расчетом всех параметров
качества детали (изделия), необходимостью расчета процесса как единой последовательности
переходов и операций (предполагая обязательное сохранение и учет эффекта
действия и результатов предшествующих этапов обработки), учетом возможности
обработки многих партий деталей, использованием многих экземпляров
оборудования, приспособлений, инструмента, решением вопросов точности, производительности
и экономичности.
При обработке деталей на станке осуществляются несколько рабочих
процессов (резание, трение), воздействующих на упругую систему, вызывая
смещение деталей, образующих подвижное соединение, в котором протекает
рабочий процесс. Но наблюдается и обратное воздействие. Например, при смещениях
инструмента и заготовки изменяется глубина и сила резания. Это заставляет рассматривать
динамическую систему как замкнутую с отрицательной обратной связью. В
замкнутой системе силы резания являются внутренними воздействиями.
Проанализируем влияние на систему внешних воздействий. Периодические силы
возникают из-за погрешностей зубчатых передач, неуравновешенности вращающихся
деталей, передаваемых фундаменту станка от другого оборудования, и т. п.;
внешние воздействия на процесс резания связаны с переменностью сечения
срезаемого слоя, скорости резания при обтачивании торцов и т. п.
Введение понятия о замкнутости системы является основным при анализе виброустойчивости и других вопросов. В ряде случаев наличие
обратной связи не учитывают и тогда силы резания считают внешним силовым фактором.
Применяемые при анализе математические методы зависят от вида системы.
Систему, которая на одно и то же входное воздействие всегда отвечает
определенным выходным воздействием, называют детерминированной. В том случае,
когда свойства оператора системы не зависят от времени, оператор и систему
называют стационарными. В стационарной системе при любом сдвиге во времени
входного возмущения без изменения его формы выходное воздействие претерпевает
такой же сдвиг во времени без изменения своей формы. Если при одном входном
воздействии выходное воздействие различно, систему называют
недетерминированной; если это выходное воздействие подчиняется явно выраженным
статистическим (вероятностным) закономерностям, то систему Называют
стохастической.
Цель расчета. При расчетах точности обработки можно:
оценить возможное рассеяние заданного параметра (вычислить суммарную
погрешность обработки);
установить долю элементарных погрешностей,
разработать мероприятия, снижающие влияние доминирующих погрешностей на точность
обработки (принимают, например, другие варианты базирования, закрепления деталей;
вместо многорезцовой обработки нежестких деталей вводят обработку на гидрокопировальных
станках и т. п.);
регламентировать продолжительность обработки деталей до принудительной
подрегулировки или смены режущего инструмента,
наиболее изнашивающихся деталей приспособления и т. п.
Наиболее сложно вычислить суммарную погрешность обработки. Это
объясняется недостаточным количеством данных по элементарным погрешностям
обработки, отсутствием частных методик по расчету технологических процессов
на точность. Поэтому технологу в некоторых случаях приходится самостоятельно
разрабатывать план, анализировать результаты теоретических и экспериментальных
исследований. Обычно ограничиваются решением двух последних задач, так как уже
это дает большой эффект в повышении точности обработки, особенно для автоматизированного
производства. Для операций, выполняемых на токарных, расточных и других
станках, расчет может быть выполнен в полном объеме. В наиболее сложных случаях
для снижения трудоемкости расчет целесообразно выполнять на вычислительных
машинах.
Основные элементарные погрешности обработки. При обработке детали кроме необходимого для
формирования поверхности движения инструмента возникают добавочные относительные
смешения детали (заготовки) и инструмента с номинальной траектории. В
результате обработанная поверхность будет иметь размер, форму и расположение, отличные от заданных.
Смещения отсчитывают от определенной базы - так называемой поверхности
отсчета—в установленном направлении. Обычно систему отсчета связывают с
номинальной обрабатываемой поверхностью. Для удобства за поверхность отсчета
можно принимать и иную поверхность, эквидистантно
расположенную относительно номинальной. Например,
при анализе погрешностей обработки поверхностей вращения за поверхность
отсчета принимают идеально расположенную ось детали.
Появление дополнительных смещений элементов технологической системы
связано с действием на систему различных тепловых, силовых и иных факторов.
Элементарные погрешности обработки характеризуют смещения одного или
нескольких элементов технологической системы под влиянием одного или нескольких
факторов.
Различают следующие основные погрешности:
∆εу — установки
заготовок в приспособлении с учетом колебания размеров баз, контактных
деформаций установочных баз заготовки и приспособления, точности изготовления
и износа приспособления;
∆у — колебания упругих деформаций технологической
системы под влиянием нестабильности нагрузок (сил резания, сил инерции и др.),
действующих в системе переменной жесткости;
∆н
— наладки технологической системы на выдерживаемый размер с учетом точностной характеристики применяемого метода наладки;
∆и — в результате размерного износа режущего
инструмента;
∑∆ст
— станка, влияющие на выдерживаемый параметр, с учетом износа станка за период
эксплуатации;
∑∆т - колебания упругих объемных и контактных
деформаций элементов технологической системы вследствие их нагрева при резании,
трения подвижных элементов системы, изменения Температуры в цехе. Такое представление
об элементарных погрешностях является условным и обосновано главным образом
удобством их расчета. В некоторых случаях можно определять отдельно
погрешности, влияющие на точность обработки. Погрешность измерения в общем
случае учитывают в составе погрешности наладки, но при значительном влиянии на
общую погрешность ее также рассматривают отдельно.
На суммарную погрешность обработки могут влиять также остаточные
напряжения от предшествующей обработки или присущие данной операции факторы
(например, скорость и продолжительность съема материала при чистовых и
отделочных операциях).
Расчет суммарной погрешности обработки. Расчетные соотношения оценки точности параметра
устанавливают путем суммирования факторов, учитываемых при анализе данного
параметра (размера, отклонения формы, расположения поверхностей). Закон
суммирования определяется природой этих погрешностей.
Примем, что исследуемый параметр детали Y представляет собой функцию нескольких переменных Хn: Y=f(X1, X2, Х3,...,Хn). Для идеальных условий соответственно имеем
Y0 = f(X10,…,Xi0,…Xn0).
В реальных условиях значения параметров отличаются от идеальных
(номинальных) на абсолютную погрешность ∆i = (X — Х0)i. Выходной параметр также может иметь некоторую
погрешность. При расчете линейных систем предполагается, что отклонения параметров
малы и взаимно независимы. Произведениями погрешностей пренебрегаем. Функцию Y = f(Xi)
в окрестностях номинальных значений параметров разложим в ряд Тейлора.
Ограничиваясь учетом только погрешности в первой степени, получим выражение для
расчета абсолютной погрешности выходного параметра Y:
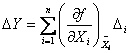 .
.
Индексы при частных производных 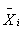 показывают, что
значения производных при Xi равны
среднему значению
показывают, что
значения производных при Xi равны
среднему значению 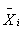 или математическому
ожиданию MXi (идеальному,
номинальному значению).
или математическому
ожиданию MXi (идеальному,
номинальному значению).
Отношение ∂f/∂Xi = Si называют
абсолютной чувствительностью функции цепи к изменению параметра, или
коэффициентом влияния, передаточным отношением.
При расчете наихудшего случая элементарные погрешности суммируют по
методу максимума-минимума:
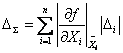 .
.
Приведенное выражение удобно для расчета, когда все параметры имеют
одинаковые единицы измерения. При разных единицах измерения параметров
целесообразно пользоваться относительными погрешностями:
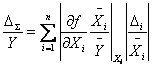 .
.
Повышение точности обработки может быть достигнуто повышением точности
каждого параметра и сокращением числа входных параметров, влияющих на отклонение
выходного параметра; уменьшением чувствительности системы к входным воздействиям
и условиям обработки; применением автоматической системы компенсации всех или
доминирующих входных параметров.
Рассмотренный метод расчета не учитывает реальных комбинаций
параметров, поэтому он дает завышенное в 1,5 — 10 раз значение погрешности
выходного параметра.
При вероятностном методе расчета отклонения ∆Y, ∆i рассматривают как случайные величины.
Для любого числа параметров i = n систематическая погрешность, равная математическому
ожиданию М(Y) = m∑, определяется по соотношению
 ,
,
где Т— допуск; α — коэффициент относительной асимметрии; E —
координата середины заданного поля допуска.
Если между погрешностями, рассматриваемыми попарно, например между ∆j и ∆i, существует стохастическая (вероятностная) связь с
коэффициентом корреляции rji, то суммарная погрешность обработки
 ,
,
где m — число попарно стохастически
связанных параметров.
Формула действительна для определения абсолютной и относительной
суммарной погрешностей.
Коэффициент относительного рассеяния, характеризующий отношение поля
рассеяния погрешности при нормальном законе распределения к действительному
полю рассеяния, обозначим Кi, где i —
индекс элементарной погрешности. Для нормального закона
распределения Кi = 1; для закона равной вероятности Кi
= 1,73; при композиции закона равной вероятности и нормального закона Ki = 1,2 ÷ 1,5 (Кi = 1,2 при l/6σ = 1, где l — приращение размера вследствие переменной
систематической погрешности; σ — среднее квадратическое отклонение; Ki = 1,5 при l/6σ = 3); для законов
Симпсона Кi = 1,22; Релея Кi = 1,097 и Максвелла Ki = 1,13.
Элементарные погрешности, изменяющиеся во времени t, являются
случайными функциями времени (например, погрешность, связанная с износом
инструмента). Тогда
 .
.
Более точный результат может быть получен при применении аппарата
случайных функций.
Часто при расчетах Si = 1;
если погрешности независимы и не зависят от времени,
 .
.
Пользуясь приведенной зависимостью, погрешность диаметра цилиндра
рассчитывают по формуле
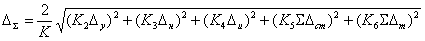 .
.
Элементарное смещение центра обрабатываемого профиля ∆εy,
возникающее при установке детали в приспособления и из-за пространственной
погрешности приспособления, при этом не учитывают.
Погрешности формы в продольном сечении могут быть учтены отдельным
слагаемым ∑∆ф путем
суммирования его с погрешностью диаметрального размера, вычисленной для
определенного поперечного сечения.
Для линейных размеров, координирующих положение обрабатываемого профиля
относительно другой поверхности детали,
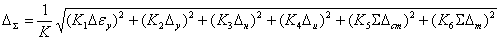 .
.
При расчетах по последним двум формулам можно принять К1 = К2
= К3 = 1 и К4 =
К5 = К6 = 1,73.
При расчетах ∆∑ часто удобнее анализировать не
отдельные элементарные погрешности, а комплексы погрешностей. Например, при
установке деталей на пальцах с зазором вычисляют комплексную погрешность,
учитывающую точность базового отверстия и установочного пальца
приспособления. Жесткость и отжатия узлов токарного
станка определяют с учетом деформации в стыках отверстие — центр станка и т. п.
Приведенное выше описание вероятностного метода суммирования позволяет
получить достоверные значения m∑ и ∆∑.
Однако в некоторых случаях данных для подобного анализа недостаточно, поэтому
ограничиваются приближенной оценкой суммарной погрешности, принимая Кi
= 1 и ∆∑ = 1/К ∙ 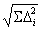 .
.
Метод квадратичного суммирования дает заниженную до 6 раз суммарную
погрешность выходного параметра.
В указанных выше формулах коэффициент 1/К (К —
коэффициент относительного рассеяния выходного параметра) корректирует суммарную
погрешность для заданной гарантированной надежности Рr:
Рr... 0,70 0,80 0,90 0,95
1/K… 0.347 0.427 0.548 0.683
Pr… 0.98 0.9973 0.9995 0.99999
1/K… 0.775 1.000 1.167 1.470
Иногда суммарную погрешность определяют смешанным методом расчета.
Принимают, что некоторые параметры изменяются детерминированно,
поэтому суммирование их выполняют по методу максимума-минимума; для других
учитываемых факторов применяют вероятностное суммирование.
Некоторые погрешности, например погрешности результата измерения,
погрешности линейного позиционирования станков с ЧПУ и других, рассчитывают с
учетом неисключенных систематических и случайных
погрешностей. Методику определения суммарной погрешности устанавливает ГОСТ
8.207 — 76. Группу результатов прямых измерений с многократными наблюдениями
подвергают статистической обработке: исключают грубые погрешности (для
результатов наблюдений, которые можно считать принадлежащими нормальному
распределению,— по методике, изложенной в ГОСТ 11.002 — 73) и известные
систематические погрешности; вычисляют
среднее арифметическое исправленных результатов наблюдений, принимаемое за
результат измерения  ; вычисляют оценку среднего квадратического
отклонения σ(
; вычисляют оценку среднего квадратического
отклонения σ( ) результата измерения;
) результата измерения;
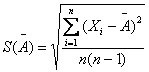 ,
,
где Xi — i-й результат наблюдения; i = 1 ÷
n.
Далее проверяют гипотезу о том, что результаты наблюдений принадлежат нормальному
распределению (уровень значимости q принимают
10—2%). При числе результатов наблюдений n > 50 проверку ведут по критерию χ2 Пирсона или ω2
Мизеса — Смирнова (ГОСТ 11.006-74); при 50 > n >
15 - по составному критерию (ГОСТ 8.207—76); при n ≤ 15
проверку не делают. Излагаемую методику можно применять, если заранее
известно, что результаты наблюдений принадлежат нормальному распределению.
Доверительные границы ε случайной составляющей
погрешности результата измерения (без учета знака) находят с помощью коэффициента
Стьюдента t (доверительную
вероятность принимают р = 0,95; в некоторых случаях
р = 0,99 и
выше):
ε = tS( ).
).
Вычисляют доверительные границы неисключенной
(неисключенных остатков) систематической погрешности
результата измерения. При суммировании составляющие этой погрешности
рассматривают как случайные величины. При отсутствии данных о виде распределения
случайных величин их распределение принимают за
равномерное. При этом условии границы неисключенной
систематической погрешности (без учета знака)

где θi — граница i-й неисключенной систематической
погрешности; К - коэффициент, определяемый
принятой доверительной вероятностью р.
При р = 0,95
принимают K = 1,1; при р = 0,99 и m > 4 принимают К = 1,4. Доверительную
вероятность для вычисления границы θ принимают так же, как и при вычислении ε.
Расчет завершается вычислением доверительных границ погрешности
результата измерения ∆. Возможны три случая.
Случай 1. При θ/S( ) < 0,8 погрешностями
θ по
сравнению с S(
) < 0,8 погрешностями
θ по
сравнению с S( ) пренебрегают и
принимают, что граница погрешности результата измерения ∆ = ε = tS(
) пренебрегают и
принимают, что граница погрешности результата измерения ∆ = ε = tS( ).
).
Случай 2. При θ/S( ) > 0,8 погрешностью
S(
) > 0,8 погрешностью
S( ) по сравнению с θ
пренебрегают и принимают ∆ =
θ. Погрешность при этих допущениях не
превышает 15%.
) по сравнению с θ
пренебрегают и принимают ∆ =
θ. Погрешность при этих допущениях не
превышает 15%.
Случай 3. Указанные неравенства не выполняются. Границы погрешности
результата измерения допускается вычислять по формуле
∆ = KS∑,
где К - коэффициент, зависящий от
соотношения случайной и неисключенной систематической
погрешностей;
 ,
,
S∑ — оценка суммарного среднего квадратического
результата измерения;
 .
.
Выше среднее квадратическое отклонение суммы неисключенных систематических погрешностей обозначено
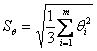 .
.
При косвенных измерениях величины X, являющейся функцией (ГОСТ 8.381-80) X
= F(Y1, Y2, ..., Ym), оценка среднего квадратического
отклонения результата косвенных измерений
 ,
,
где Si(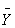 i) — оценка среднего квадратического
отклонения результата измерения Yi.
i) — оценка среднего квадратического
отклонения результата измерения Yi.
Граница неисключенной систематической
погрешности ∆Yi измерения
величины Yi
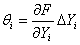
Расчет ∆ ведут далее по указанным выше формулам, при этом
учитывают все неисключенные систематические
составляющие θi, где i = l, 2,...,N.
Эффективным способом вычисления суммарной погрешности является
статистическое моделирование, при котором используют ЭВМ (методы Монте-Карло).
При этом методе определяют псевдослучайные значения факторов и с помощью ЭВМ
погрешность выходного параметра. Статистические свойства системы оценивают
путем многократного построения процесса. Метод допускает произвольное
распределение параметров. Метод Монте-Карло применяют для систем массового
производства; он может быть легко запрограммирован, но при этом требуется
относительно большое время счета.
Аналитическое представление реальной поверхности позволяет более четко
выявить законы суммирования отклонений размера и формы поверхности. Различают
номинальные геометрические поверхности, имеющие предписанные чертежом формы и
размеры, без каких бы то ни было неровностей и отклонений, и действительные
(реальные) поверхности деталей. Понимая под профилем линию пересечения
поверхности плоскостью, ориентированной определенным образом, различают также
номинальный и действительный профили детали.
При исследовании точности обработки деталей с номинальной
цилиндрической поверхностью широко используют методы спектральной теории
неровностей и других геометрических параметров.
Введем понятие о текущем размере как о радиусе-векторе,
равном расстоянию от точки на реальном профиле до геометрического центра
номинального профиля детали. Очевидно, что в общем случае радиус-вектор R
зависит
от угловой координаты φ точки и координаты z, направленной вдоль оси: R = F (φ, z).
Если номинальный радиус поверхности обозначить как Ro,
то функция f(φ, z), изображающая погрешность (абсолютная погрешность ∆R), в общем случае (при 0 ≤ z
≤ l), где l —
длина поверхности) характеризует отклонение от цилиндричности
f(φ, z) = R — Ro = ∆R, а в поперечном сечении (при z = zi) — отклонение от круглости;
f(φ) = R – R0 = ∆R.
Функцию погрешности поперечного сечения приближенно можно представить
в виде ряда Фурье с конечным числом членов k = n:
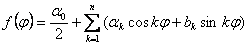
или
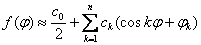 ,
,
где αk, bk, ck - коэффициенты
ряда Фурье; k — порядковый номер составляющей гармоники.
Контур поперечного сечения удовлетворяет условию замкнутости; период
равен 2π: f(φ + 2π) = f(φ).
Коэффициенты ряда Фурье
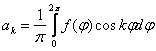 ;
;
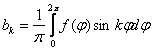
Между амплитудой k-й гармоники ck
и коэффициентами ak и bk, а также начальной фазой φk существуют зависимости:
ak = ckcosφk;
bk = cksinφk;
ck = 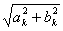 ;
;
tgφk = bk / ak;
c0 = a0 =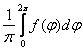 .
.
Члены разложения имеют явный физический смысл. Нулевой член, т. е.
величина со/2, равен
среднему значению функции на период Т = 2π. Эта величина характеризует отклонение
собственно размера, являясь постоянной (независимой от угловой координаты φ) составляющей
текущего размера. Первый член разложения c1cos(φ + φ1) характеризует отклонение расположения реального и
номинального профилей (эксцентриситет с амплитудой с1
и фазой φ1. Следующие члены ряда
Фурье характеризуют; c2cos(2φ + φ2) — овальность, c3cos(3φ + φ3) — огранку с трехвершинным профилем и т. п.
Таким образом, члены ряда при k = 1 ÷
р характеризует спектр отклонений формы детали в
поперечном сечении: последующие члены ряда — волнистость и при достаточно больших
значениях k — шероховатость поверхности. Аналогичный метод может
быть применен к профилю цилиндрической детали.
Изложенная методика позволяет проанализировать
отклонения собственно размера (∆R или 2∆R = ∆D) формы и
т. д., рассматриваемые как систематические отклонения. Методику можно
использовать при рассмотрении детерминированных систем. Однако в общем случае
амплитуды и фазы отклонений являются случайными величинами. Вероятностные
методы суммирования отклонений для поперечного сечения номинально
цилиндрической поверхности рассмотрены ниже.
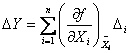 .
.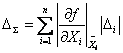 .
.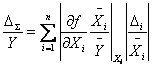

 .
.
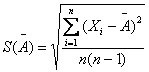 ,
,

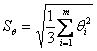

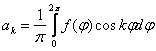 ;
;